堆的 shift down
本小节将介绍如何从一个最大堆中取出一个元素,称为 shift down,只能取出最大优先级的元素,也就是根节点,把原来的 62 取出后,下面介绍如何填补这个最大堆。
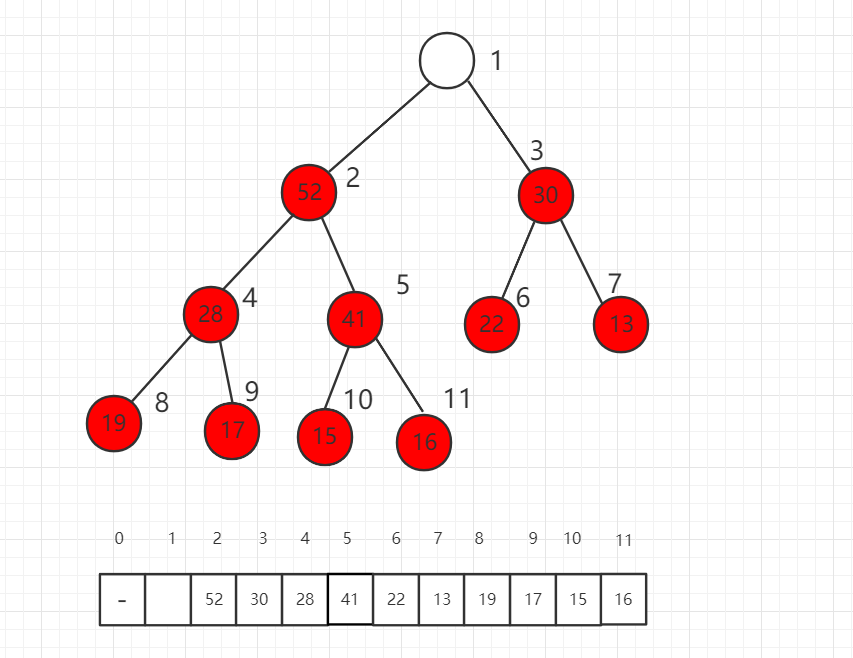
第一步,我们将数组最后一位数组放到根节点,此时不满足最大堆的定义。
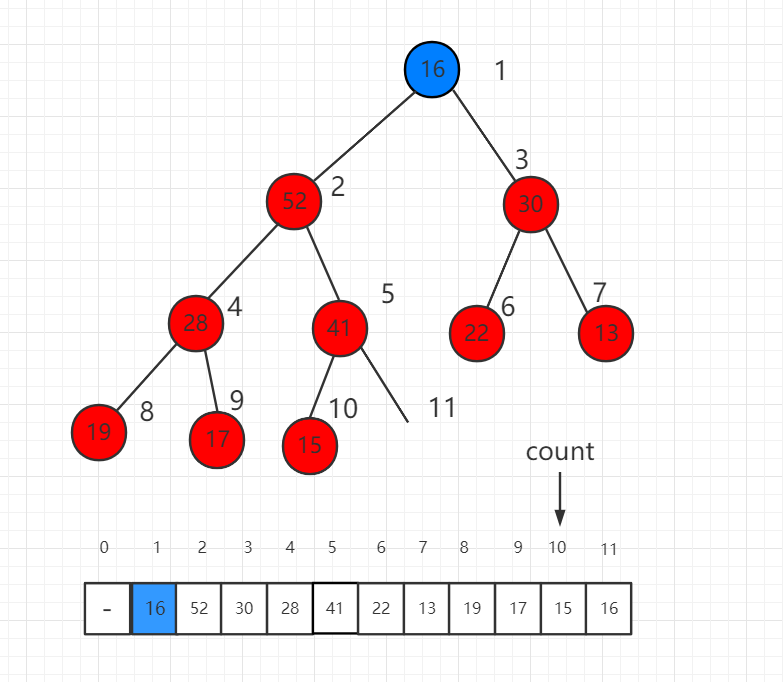
调整的过程是将这个根节点 16 一步一步向下挪,16 比子节点都小,先比较子节点 52 和 30 哪个大,和大的交换位置。
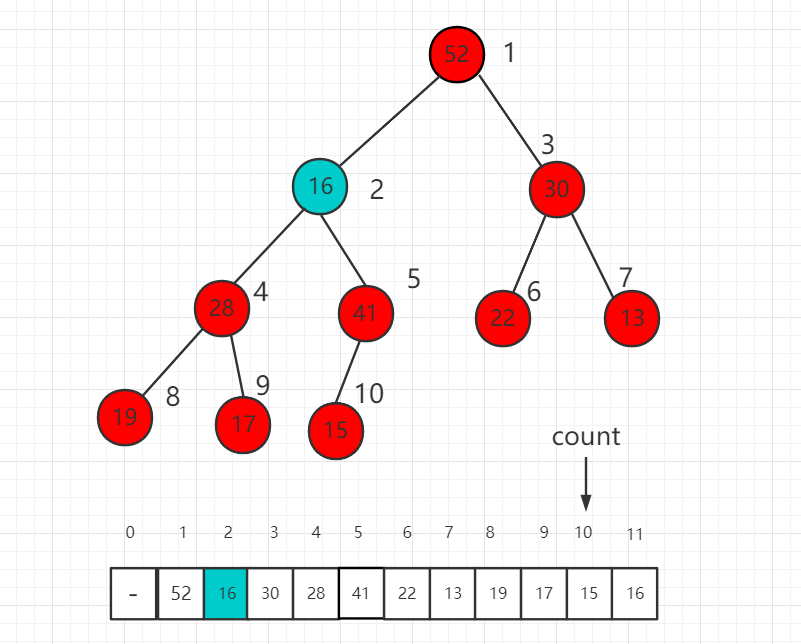
继续比较 16 的子节点 28 和 41,41 大,所以 16 和 41 交换位置。
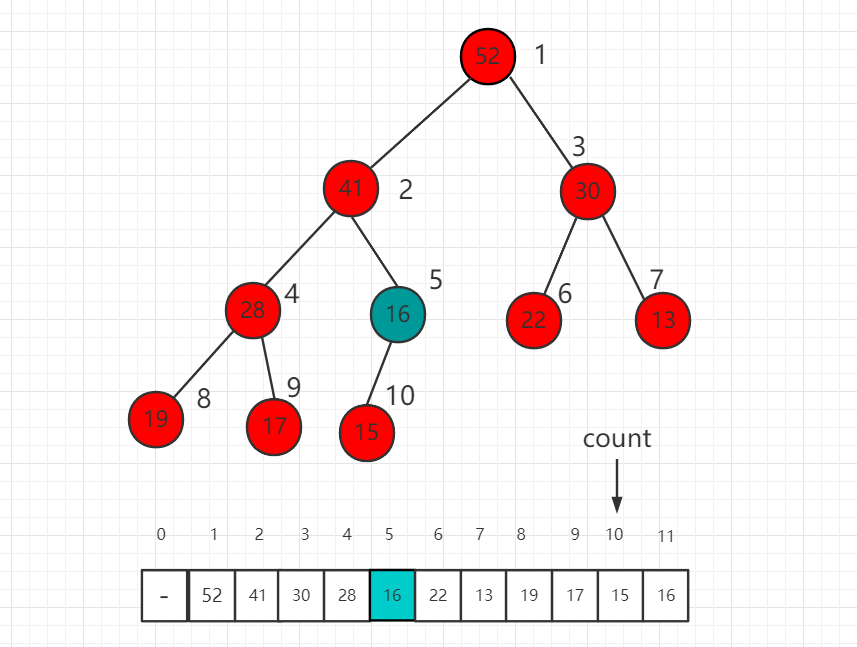
继续 16 和孩子节点 15 进行比较,16 大,所以现在不需要进行交换,最后我们的 shift down 操作完成,维持了一个最大堆的性质。
四、Java 实例代码
源码包下载:Download
src/runoob/heap/HeapShiftDown.java 文件代码:
package runoob.heap;
/**
* 往最大堆中取出一个元素
*/
public class HeapShiftDown<T extends Comparable> {
protected T[] data;
protected int count;
protected int capacity;
// 构造函数, 构造一个空堆, 可容纳capacity个元素
public HeapShiftDown(int capacity){
//这里加1是指原来能装的元素个数,那去掉0位,只能装capacity个元素
data = (T[])new Comparable[capacity+1];
count = 0;
this.capacity = capacity;
}
// 返回堆中的元素个数
public int size(){
return count;
}
// 返回一个布尔值, 表示堆中是否为空
public boolean isEmpty(){
return count == 0;
}
// 像最大堆中插入一个新的元素 item
public void insert(T item){
assert count + 1 <= capacity;
data[count+1] = item;
count ++;
shiftUp(count);
}
// 从最大堆中取出堆顶元素, 即堆中所存储的最大数据
public T extractMax(){
assert count > 0;
T ret = data[1];
swap( 1 , count );
count --;
shiftDown(1);
return ret;
}
// 获取最大堆中的堆顶元素
public T getMax(){
assert( count > 0 );
return data[1];
}
// 交换堆中索引为i和j的两个元素
private void swap(int i, int j){
T t = data[i];
data[i] = data[j];
data[j] = t;
}
//********************
//* 最大堆核心辅助函数
//********************
private void shiftUp(int k){
while( k > 1 && data[k/2].compareTo(data[k]) < 0 ){
swap(k, k/2);
k /= 2;
}
}
//shiftDown操作
private void shiftDown(int k){
while( 2*k <= count ){
int j = 2*k; // 在此轮循环中,data[k]和data[j]交换位置
if( j+1 <= count && data[j+1].compareTo(data[j]) > 0 )
j ++;
// data[j] 是 data[2*k]和data[2*k+1]中的最大值
if( data[k].compareTo(data[j]) >= 0 ) break;
swap(k, j);
k = j;
}
System.out.println("shiftDown结束");
}
// 测试 HeapShiftDown
public static void main(String[] args) {
HeapShiftDown<Integer> heapShiftDown = new HeapShiftDown<Integer>(100);
// 堆中元素个数
int N = 100;
// 堆中元素取值范围[0, M)
int M = 100;
for( int i = 0 ; i < N ; i ++ )
heapShiftDown.insert( new Integer((int)(Math.random() * M)) );
Integer[] arr = new Integer[N];
// 将最大堆中的数据逐渐使用extractMax取出来
// 取出来的顺序应该是按照从大到小的顺序取出来的
for( int i = 0 ; i < N ; i ++ ){
arr[i] = heapShiftDown.extractMax();
System.out.print(arr[i] + " ");
}
// 确保arr数组是从大到小排列的
for( int i = 1 ; i < N ; i ++ )
assert arr[i-1] >= arr[i];
}
}
/**
* 往最大堆中取出一个元素
*/
public class HeapShiftDown<T extends Comparable> {
protected T[] data;
protected int count;
protected int capacity;
// 构造函数, 构造一个空堆, 可容纳capacity个元素
public HeapShiftDown(int capacity){
//这里加1是指原来能装的元素个数,那去掉0位,只能装capacity个元素
data = (T[])new Comparable[capacity+1];
count = 0;
this.capacity = capacity;
}
// 返回堆中的元素个数
public int size(){
return count;
}
// 返回一个布尔值, 表示堆中是否为空
public boolean isEmpty(){
return count == 0;
}
// 像最大堆中插入一个新的元素 item
public void insert(T item){
assert count + 1 <= capacity;
data[count+1] = item;
count ++;
shiftUp(count);
}
// 从最大堆中取出堆顶元素, 即堆中所存储的最大数据
public T extractMax(){
assert count > 0;
T ret = data[1];
swap( 1 , count );
count --;
shiftDown(1);
return ret;
}
// 获取最大堆中的堆顶元素
public T getMax(){
assert( count > 0 );
return data[1];
}
// 交换堆中索引为i和j的两个元素
private void swap(int i, int j){
T t = data[i];
data[i] = data[j];
data[j] = t;
}
//********************
//* 最大堆核心辅助函数
//********************
private void shiftUp(int k){
while( k > 1 && data[k/2].compareTo(data[k]) < 0 ){
swap(k, k/2);
k /= 2;
}
}
//shiftDown操作
private void shiftDown(int k){
while( 2*k <= count ){
int j = 2*k; // 在此轮循环中,data[k]和data[j]交换位置
if( j+1 <= count && data[j+1].compareTo(data[j]) > 0 )
j ++;
// data[j] 是 data[2*k]和data[2*k+1]中的最大值
if( data[k].compareTo(data[j]) >= 0 ) break;
swap(k, j);
k = j;
}
System.out.println("shiftDown结束");
}
// 测试 HeapShiftDown
public static void main(String[] args) {
HeapShiftDown<Integer> heapShiftDown = new HeapShiftDown<Integer>(100);
// 堆中元素个数
int N = 100;
// 堆中元素取值范围[0, M)
int M = 100;
for( int i = 0 ; i < N ; i ++ )
heapShiftDown.insert( new Integer((int)(Math.random() * M)) );
Integer[] arr = new Integer[N];
// 将最大堆中的数据逐渐使用extractMax取出来
// 取出来的顺序应该是按照从大到小的顺序取出来的
for( int i = 0 ; i < N ; i ++ ){
arr[i] = heapShiftDown.extractMax();
System.out.print(arr[i] + " ");
}
// 确保arr数组是从大到小排列的
for( int i = 1 ; i < N ; i ++ )
assert arr[i-1] >= arr[i];
}
}
