支持向量机
支持向量机(Support Vector Machine,简称 SVM)是一种监督学习算法,主要用于分类和回归问题。
SVM 的核心思想是找到一个最优的超平面,将不同类别的数据分开。这个超平面不仅要能够正确分类数据,还要使得两个类别之间的间隔(margin)最大化。
超平面:
- 在二维空间中,超平面是一个直线。
- 在三维空间中,超平面是一个平面。
- 在更高维空间中,超平面是一个分割空间的超平面。
支持向量:
- 支持向量是离超平面最近的样本点。这些支持向量对于定义超平面至关重要。
- 支持向量机通过最大化支持向量到超平面的距离(即最大化间隔)来选择最佳的超平面。
最大间隔:
- SVM的目标是最大化分类间隔,使得分类边界尽可能远离两类数据点。这可以有效地减少模型的泛化误差。
核技巧(Kernel Trick):
- 对于非线性可分的数据,SVM使用核函数将数据映射到更高维的空间,在这个空间中,数据可能是线性可分的。
- 常用的核函数有:线性核、多项式核、径向基函数(RBF)核等。
SVM 分类流程
- 选择一个超平面:找到一个能够最大化分类边界的超平面。
- 训练支持向量:通过支持向量机算法,选择离超平面最近的样本点作为支持向量。
- 通过最大化间隔来找到最优超平面:选择一个最优超平面,使得间隔最大化。
- 使用核函数处理非线性问题:通过核函数将数据映射到高维空间来解决非线性可分问题。
使用 Python 实现 SVM
接下来,我们将使用 Python 中的 scikit-learn 库来实现一个简单的 SVM 分类器。
1. 安装必要的库
首先,确保你已经安装了scikit-learn库。如果没有安装,可以使用以下命令进行安装:
pip install scikit-learn
2. 导入库
实例
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
from sklearn import svm, datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
3. 加载数据集
我们将使用scikit-learn自带的鸢尾花(Iris)数据集。
实例
# 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data[:, :2] # 只使用前两个特征
y = iris.target
iris = datasets.load_iris()
X = iris.data[:, :2] # 只使用前两个特征
y = iris.target
4. 划分训练集和测试集
实例
# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
5. 训练 SVM 模型
实例
# 创建SVM分类器
clf = svm.SVC(kernel='linear') # 使用线性核函数
# 训练模型
clf.fit(X_train, y_train)
clf = svm.SVC(kernel='linear') # 使用线性核函数
# 训练模型
clf.fit(X_train, y_train)
6. 预测与评估
实例
# 在测试集上进行预测
y_pred = clf.predict(X_test)
# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"模型准确率: {accuracy:.2f}")
y_pred = clf.predict(X_test)
# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"模型准确率: {accuracy:.2f}")
7. 可视化结果
实例
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data[:, :2] # 只使用前两个特征
y = iris.target
# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 创建SVM分类器
clf = svm.SVC(kernel='linear') # 使用线性核函数
# 训练模型
clf.fit(X_train, y_train)
# 在测试集上进行预测
y_pred = clf.predict(X_test)
# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"模型准确率: {accuracy:.2f}")
# 绘制决策边界
def plot_decision_boundary(X, y, model):
h = .02 # 网格步长
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o')
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.title('SVM Decision Boundary')
plt.show()
plot_decision_boundary(X_train, y_train, clf)
import matplotlib.pyplot as plt
from sklearn import svm, datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data[:, :2] # 只使用前两个特征
y = iris.target
# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 创建SVM分类器
clf = svm.SVC(kernel='linear') # 使用线性核函数
# 训练模型
clf.fit(X_train, y_train)
# 在测试集上进行预测
y_pred = clf.predict(X_test)
# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"模型准确率: {accuracy:.2f}")
# 绘制决策边界
def plot_decision_boundary(X, y, model):
h = .02 # 网格步长
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o')
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.title('SVM Decision Boundary')
plt.show()
plot_decision_boundary(X_train, y_train, clf)
执行以上代码,输出为:
模型准确率: 0.80
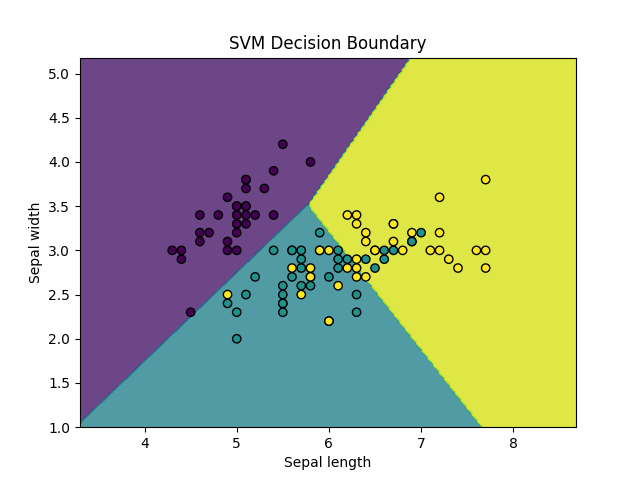
图片显示为: