插入排序
插入排序(InsertionSort)，一般也被称为直接插入排序，对于少量元素的排序，它是一个有效的算法。
插入排序是一种最简单的排序方法，它的基本思想是将一个记录插入到已经排好序的有序表中，从而一个新的、记录数增 1 的有序表。
在其实现过程使用双层循环，外层循环对除了第一个元素之外的所有元素，内层循环对当前元素前面有序表进行待插入位置查找，并进行移动。
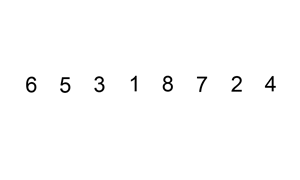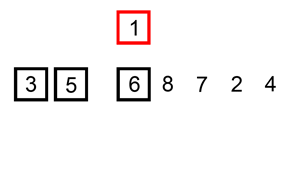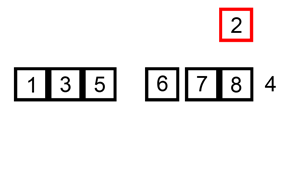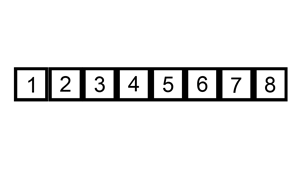
工作原理
插入排序的核心思想是 "构建有序序列"。它将待排序的数组（或列表）在逻辑上分为两个部分：
- 已排序部分：初始时，通常认为数组的第一个元素自身就是一个有序序列。
- 未排序部分：从第二个元素开始到最后一个元素。
算法会 反复地将未排序部分的第一个元素，插入到已排序部分的正确位置，直到未排序部分为空，整个数组就变得有序了。
适用说明
插入排序的平均时间复杂度也是 O(n^2)，空间复杂度为常数阶 O(1)，具体时间复杂度和数组的有序性也是有关联的。
插入排序中，当待排序数组是有序时，是最优的情况，只需当前数跟前一个数比较一下就可以了，这时一共需要比较 N-1 次，时间复杂度为 O(N)。最坏的情况是待排序数组是逆序的，此时需要比较次数最多，最坏的情况是 O(n^2)。
过程图示
假设前面 n-1(其中 n>=2)个数已经是排好顺序的，现将第 n 个数插到前面已经排好的序列中，然后找到合适自己的位置，使得插入第n个数的这个序列也是排好顺序的。
按照此法对所有元素进行插入，直到整个序列排为有序的过程，称为插入排序。
从小到大的插入排序整个过程如图示：
第一轮：从第二位置的 6 开始比较，比前面 7 小，交换位置。
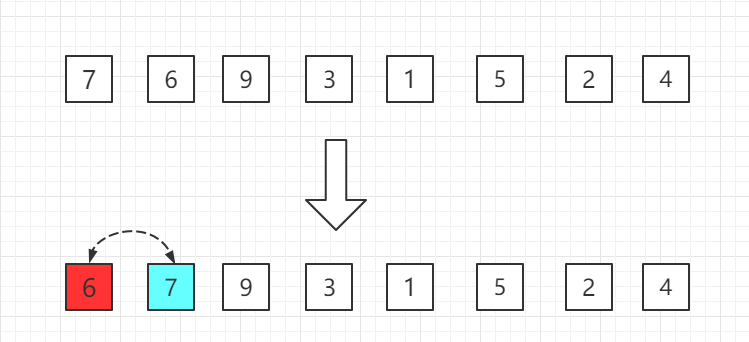
第二轮：第三位置的 9 比前一位置的 7 大，无需交换位置。
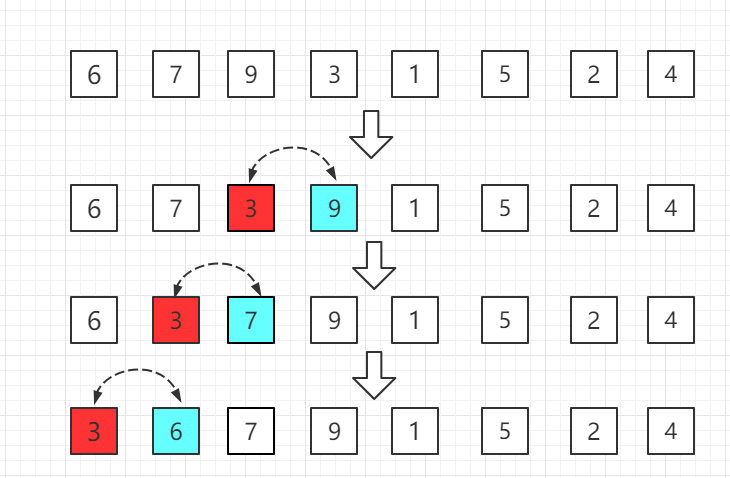
第三轮：第四位置的 3 比前一位置的 9 小交换位置，依次往前比较。
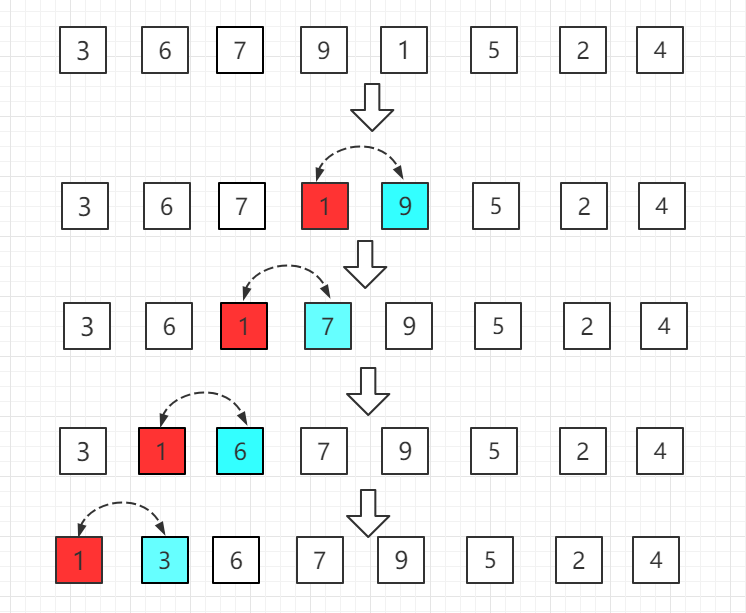
第四轮：第五位置的 1 比前一位置的 9 小，交换位置，再依次往前比较。
......
就这样依次比较到最后一个元素。
算法实现与代码解析
理解了原理后，我们来看具体的代码实现。这里提供 Python 和 Java 两种常见语言的版本。
Python 实现
实例
"""
插入排序算法实现 (升序)
:param arr: 待排序的列表
:return: 排序后的列表 (原地修改，也返回)
"""
# 遍历从第二个元素开始到最后一个元素 (索引 1 到 n-1)
for i in range(1, len(arr)):
current_value = arr[i] # 当前需要插入的元素，先"拿在手里"
j = i - 1 # j 指向已排序序列的最后一个元素
# 内层循环：为 current_value 在已排序部分 arr[0..i-1] 中寻找插入位置
# 条件1: j >= 0 确保不越界到列表头部之前
# 条件2: arr[j] > current_value 说明当前比较的元素比"手里的"大，需要后移
while j >= 0 and arr[j] > current_value:
arr[j + 1] = arr[j] # 将较大的元素向后移动一位，腾出空位
j -= 1 # 继续向左比较下一个元素
# 循环结束，说明找到了插入位置 (j+1)
# 此时 arr[j] <= current_value 或 j == -1
arr[j + 1] = current_value # 将"手里的"元素插入到正确位置
return arr
# 测试代码
if __name__ == "__main__":
# 测试数据
test_data = [64, 34, 25, 12, 22, 11, 90]
print("排序前:", test_data)
sorted_data = insertion_sort(test_data.copy()) # 使用副本排序，不影响原数据
print("排序后:", sorted_data)
# 另一个测试：基本有序的数据
nearly_sorted_data = [1, 3, 2, 4, 6, 5, 8, 7]
print("\n基本有序数据排序前:", nearly_sorted_data)
print("基本有序数据排序后:", insertion_sort(nearly_sorted_data.copy()))
Java 实现
实例
public static void insertionSort(int[] arr) {
// 遍历从第二个元素开始到最后一个元素 (索引 1 到 n-1)
for (int i = 1; i < arr.length; i++) {
int currentValue = arr[i]; // 当前需要插入的元素
int j = i - 1; // j 指向已排序序列的最后一个元素
// 内层循环：寻找插入位置并移动元素
while (j >= 0 && arr[j] > currentValue) {
arr[j + 1] = arr[j]; // 元素后移
j--;
}
// 插入当前元素到正确位置
arr[j + 1] = currentValue;
}
}
// 重载方法，支持对整型数组的一部分进行排序
public static void insertionSort(int[] arr, int left, int right) {
for (int i = left + 1; i <= right; i++) {
int currentValue = arr[i];
int j = i - 1;
while (j >= left && arr[j] > currentValue) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = currentValue;
}
}
public static void main(String[] args) {
// 测试数据
int[] testData = {64, 34, 25, 12, 22, 11, 90};
System.out.print("排序前: ");
printArray(testData);
int[] dataToSort = testData.clone(); // 使用副本
insertionSort(dataToSort);
System.out.print("排序后: ");
printArray(dataToSort);
}
private static void printArray(int[] arr) {
for (int num : arr) {
System.out.print(num + " ");
}
System.out.println();
}
}
算法特性分析
了解一个算法的性能和应用场景至关重要。插入排序的特性可以总结如下：
| 特性 | 说明 | 解释 |
|---|---|---|
| 时间复杂度 | 平均和最坏情况：$O(n^2)$ | 需要嵌套循环比较和移动元素。对于 n 个元素，最坏情况下（完全逆序）需要约 $\frac{n(n-1)}{2}$ 次比较和移动。 |
| 最好情况：$O(n)$ | 当输入数组已经基本有序时，内层循环很少执行或立即退出，仅需进行 n-1 次比较。 | |
| 空间复杂度 | $O(1)$ | 是 原地排序 算法，只需要常数级别的额外空间（如 current_value, j 等变量）。 |
| 稳定性 | 稳定 | 当两个元素相等时，排序后它们的相对顺序保持不变。因为算法只在遇到 大于 当前值时才移动元素。 |
| 适用场景 | 1. 小规模数据 2. 数据基本有序 3. 作为高级排序算法（如快速排序、归并排序）的子过程 |
在这些情况下，其简单的逻辑和低常数开销使其表现可能优于更复杂的 $O(n \log n)$ 算法。 |
时间复杂度公式推导（最坏情况）
在最坏情况（数组完全逆序）下：
- 第 1 个元素（索引 0）插入，比较 0 次。
- 第 2 个元素（索引 1）插入，比较 1 次，移动 1 次。
- 第 3 个元素（索引 2）插入，比较 2 次，移动 2 次。
- ...
- 第 n 个元素（索引 n-1）插入，比较 n-1 次，移动 n-1 次。
总比较和移动次数为： $0 + 1 + 2 + ... + (n-1) = \frac{n(n-1)}{2}$
因此，时间复杂度为 $O(n^2)$。