淘宝双十一超级红包 》
希尔排序
一、概念及其介绍
希尔排序(Shell Sort)是插入排序的一种，它是针对直接插入排序算法的改进。
希尔排序又称缩小增量排序，因 DL.Shell 于 1959 年提出而得名。
它通过比较相距一定间隔的元素来进行，各趟比较所用的距离随着算法的进行而减小，直到只比较相邻元素的最后一趟排序为止。
二、适用说明
希尔排序时间复杂度是 O(n^(1.3-2))，空间复杂度为常数阶 O(1)。希尔排序没有时间复杂度为 O(n(logn)) 的快速排序算法快 ，因此对中等大小规模表现良好，但对规模非常大的数据排序不是最优选择，总之比一般 O(n^2 ) 复杂度的算法快得多。
三、过程图示
希尔排序目的为了加快速度改进了插入排序，交换不相邻的元素对数组的局部进行排序，并最终用插入排序将局部有序的数组排序。
在此我们选择增量 gap=length/2，缩小增量以 gap = gap/2 的方式，用序列 {n/2,(n/2)/2...1} 来表示。
如图示例：
（1）初始增量第一趟 gap = length/2 = 4
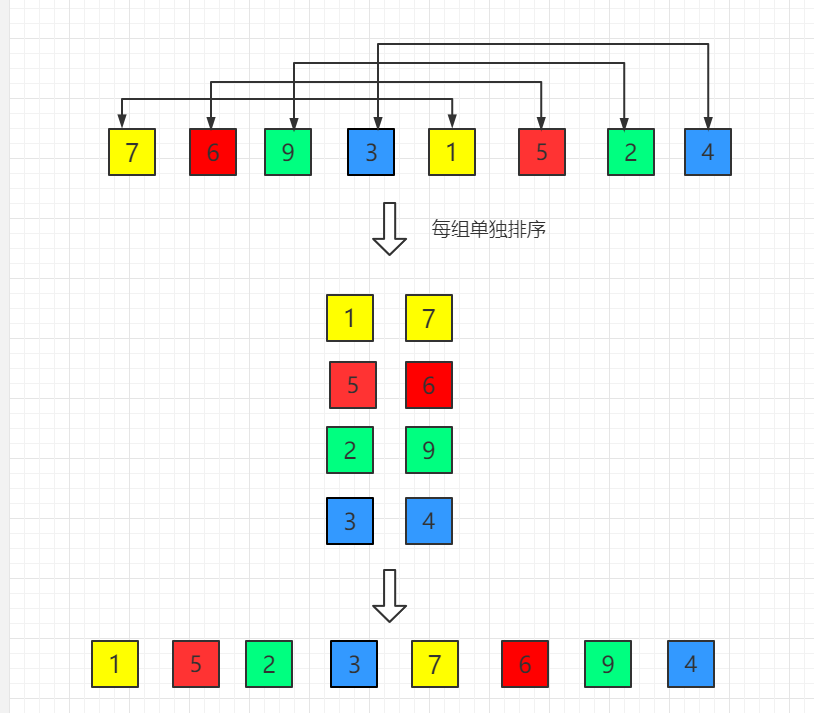
（2）第二趟，增量缩小为 2
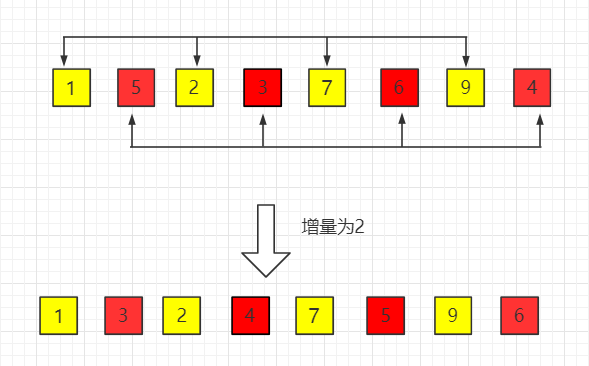
（3）第三趟，增量缩小为 1,得到最终排序结果
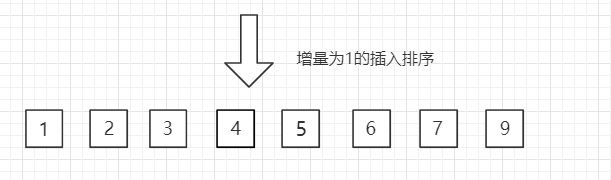
四、Java 实例代码
源码包下载：Download
最内层循环其实就是插入排序:
ShellSort.java 文件代码：
public class ShellSort {
//核心代码---开始
public static void sort(Comparable[] arr) {
int j;
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
for (int i = gap; i < arr.length; i++) {
Comparable tmp = arr[i];
for (j = i; j >= gap && tmp.compareTo(arr[j - gap]) < 0; j -= gap) {
arr[j] = arr[j - gap];
}
arr[j] = tmp;
}
}
}
//核心代码---结束
public static void main(String[] args) {
int N = 2000;
Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 10);
ShellSort.sort(arr);
for( int i = 0 ; i < arr.length ; i ++ ){
System.out.print(arr[i]);
System.out.print(' ');
}
}
}
//核心代码---开始
public static void sort(Comparable[] arr) {
int j;
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
for (int i = gap; i < arr.length; i++) {
Comparable tmp = arr[i];
for (j = i; j >= gap && tmp.compareTo(arr[j - gap]) < 0; j -= gap) {
arr[j] = arr[j - gap];
}
arr[j] = tmp;
}
}
}
//核心代码---结束
public static void main(String[] args) {
int N = 2000;
Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 10);
ShellSort.sort(arr);
for( int i = 0 ; i < arr.length ; i ++ ){
System.out.print(arr[i]);
System.out.print(' ');
}
}
}