随机化快速排序
快速排序是计算机科学中最经典的排序算法之一,以其平均情况下 O(n log n) 的时间复杂度而闻名,然而,当输入数据已经有序或接近有序时,传统的快速排序会退化到 O(n²) 的时间复杂度,随机化快速排序通过引入随机性,巧妙地解决了这个问题。
在深入随机化快速排序之前,让我们先回顾一下传统快速排序的核心思想。
快速排序的工作原理
快速排序采用 分治策略,其基本步骤如下:
- 选择基准值:从数组中选择一个元素作为基准值
- 分区操作:重新排列数组,使所有小于基准值的元素放在基准值前面,所有大于基准值的元素放在基准值后面
- 递归排序:对基准值左右两侧的子数组递归地应用相同的过程
传统快速排序的问题
传统快速排序的性能高度依赖于基准值的选择。当每次选择的基准值都能将数组大致平分为两部分时,算法效率最高。但在以下情况下,性能会显著下降:
- 已排序数组:如果数组已经有序,每次选择最后一个元素作为基准值会导致分区极度不平衡
- 逆序数组:与已排序数组类似,但方向相反
- 重复元素:大量重复元素也会导致分区不平衡
在这些最坏情况下,快速排序的时间复杂度会退化到 O(n²),与冒泡排序等简单算法相当。
随机化快速排序通过引入随机性来避免最坏情况的发生,确保算法在各种输入下都能保持较好的平均性能。
随机化快速排序的核心改进非常简单:随机选择基准值,而不是固定选择第一个、最后一个或中间的元素。这种随机性使得算法在最坏情况下的概率极低,从而保证了期望时间复杂度为 O(n log n)。
随机化快速排序基本思想:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
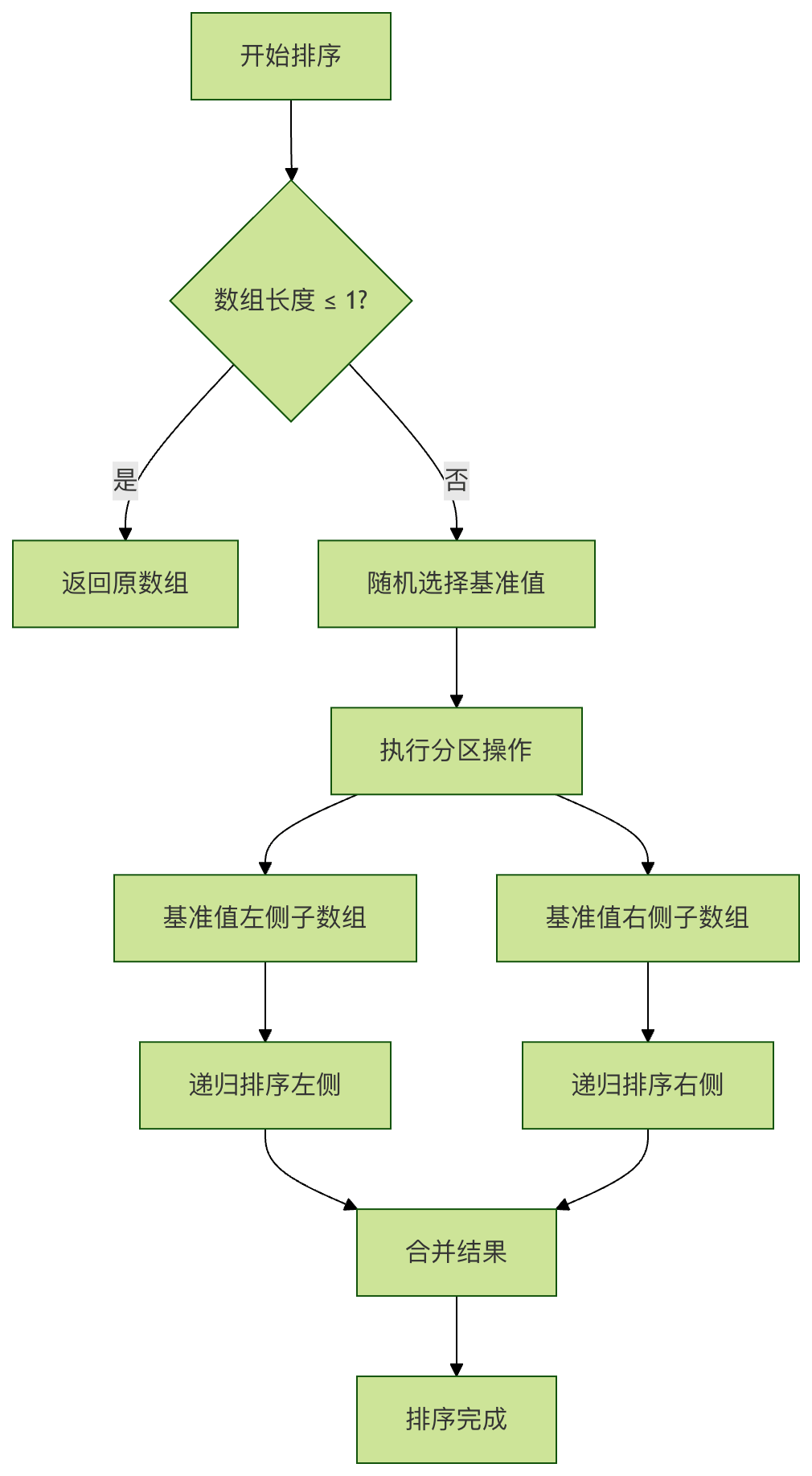
算法优势
| 特性 | 传统快速排序 | 随机化快速排序 |
|---|---|---|
| 最坏情况时间复杂度 | O(n²) | O(n²)(但概率极低) |
| 平均情况时间复杂度 | O(n log n) | O(n log n) |
| 最坏情况发生条件 | 特定输入(如已排序数组) | 随机选择恰好总是选到最值 |
| 空间复杂度 | O(log n)(递归栈) | O(log n)(递归栈) |
| 稳定性 | 不稳定 | 不稳定 |
虽然理论上随机化快速排序的最坏情况时间复杂度仍然是 O(n²),但在实际应用中,这种最坏情况发生的概率极低。对于包含 n 个元素的数组,随机选择基准值导致最坏情况的概率约为 1/n!,这在实践中几乎不可能发生。
过程图示
在一个数组中选择一个基点,比如第一个位置的 4,然后把4挪到正确位置,使得之前的子数组中数据小于 4,之后的子数组中数据大于 4,然后逐渐递归下去完成整个排序。
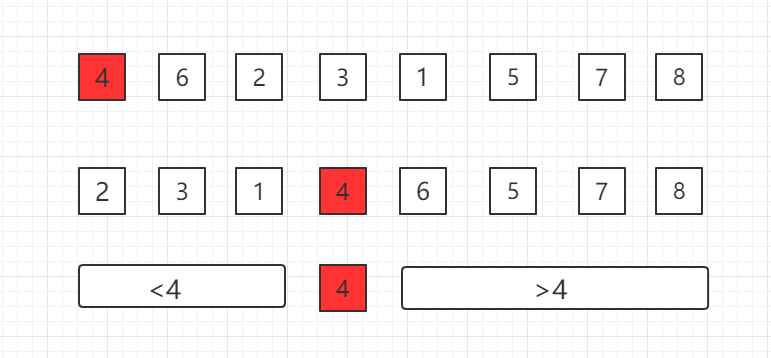
如何和把选定的基点数据挪到正确位置上,这是快速排序的核心,我们称为 Partition。
过程如下所示,其中 i 为当前遍历比较的元素位置:
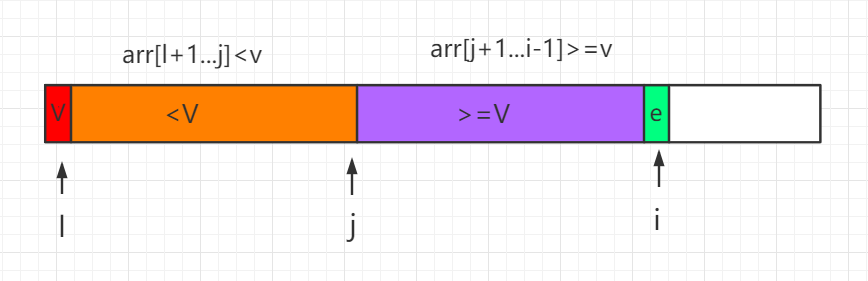
这个 partition 过程用代码表示为:
实例
private static int partition(Comparable[] arr, int l, int r){
Comparable v = arr[l];
int j = l;
for( int i = l + 1 ; i <= r ; i ++ )
if( arr[i].compareTo(v) < 0 ){
j ++;
//数组元素位置交换
swap(arr, j, i);
}
swap(arr, l, j);
return j;
}
...
如果是对近乎有序的数组进行快速排序,每次 partition 分区后子数组大小极不平衡,容易退化成 O(n^2) 的时间复杂度算法。我们需要对上述代码进行优化,随机选择一个基点做为比较,称为随机化快速排序算法。只需要在上述代码前加上下面一行,随机选择数组中一数据和基点数据进行交换。
swap( arr, l , (int)(Math.random()*(r-l+1))+l );
Java 实例代码
源码包下载:Download
QuickSort.java 文件代码:
/**
* 随机化快速排序
*/
public class QuickSort {
// 对arr[l...r]部分进行partition操作
// 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
private static int partition(Comparable[] arr, int l, int r){
// 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
swap( arr, l , (int)(Math.random()*(r-l+1))+l );
Comparable v = arr[l];
// arr[l+1...j] < v ; arr[j+1...i) > v
int j = l;
for( int i = l + 1 ; i <= r ; i ++ )
if( arr[i].compareTo(v) < 0 ){
j ++;
swap(arr, j, i);
}
swap(arr, l, j);
return j;
}
// 递归使用快速排序,对arr[l...r]的范围进行排序
private static void sort(Comparable[] arr, int l, int r){
if (l >= r) {
return;
}
int p = partition(arr, l, r);
sort(arr, l, p-1 );
sort(arr, p+1, r);
}
public static void sort(Comparable[] arr){
int n = arr.length;
sort(arr, 0, n-1);
}
private static void swap(Object[] arr, int i, int j) {
Object t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
// 测试 QuickSort
public static void main(String[] args) {
// Quick Sort也是一个O(nlogn)复杂度的算法
// 可以在1秒之内轻松处理100万数量级的数据
int N = 1000000;
Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 100000);
sort(arr);
SortTestHelper.printArray(arr);
}
}
随机化快速排序的实现
Python 实现
实例
def randomized_quick_sort(arr, low=None, high=None):
"""
随机化快速排序的主函数
参数:
arr: 待排序的列表
low: 子数组的起始索引(默认为0)
high: 子数组的结束索引(默认为len(arr)-1)
返回:
排序后的列表(原地排序,也返回排序后的列表)
"""
# 设置默认参数
if low is None:
low = 0
if high is None:
high = len(arr) - 1
# 递归终止条件:子数组长度小于等于1
if low < high:
# 随机选择基准值并分区
pivot_index = randomized_partition(arr, low, high)
# 递归排序左右子数组
randomized_quick_sort(arr, low, pivot_index - 1)
randomized_quick_sort(arr, pivot_index + 1, high)
return arr
def randomized_partition(arr, low, high):
"""
随机分区函数
参数:
arr: 待分区的列表
low: 子数组的起始索引
high: 子数组的结束索引
返回:
基准值的最终位置索引
"""
# 随机选择一个索引作为基准值位置
random_index = random.randint(low, high)
# 将随机选择的元素与最后一个元素交换
arr[random_index], arr[high] = arr[high], arr[random_index]
# 使用最后一个元素(现在是随机选择的元素)作为基准值
return partition(arr, low, high)
def partition(arr, low, high):
"""
分区函数(与快速排序相同)
参数:
arr: 待分区的列表
low: 子数组的起始索引
high: 子数组的结束索引
返回:
基准值的最终位置索引
"""
pivot = arr[high] # 基准值
i = low - 1 # 小于基准值的区域的边界
for j in range(low, high):
if arr[j] <= pivot:
i += 1
# 交换元素
arr[i], arr[j] = arr[j], arr[i]
# 将基准值放到正确的位置
arr[i + 1], arr[high] = arr[high], arr[i + 1]
return i + 1
# 测试数据
test_data = [3, 6, 8, 10, 1, 2, 1]
print("原始数组:", test_data)
print("排序后数组:", randomized_quick_sort(test_data.copy()))
时间复杂度分析
随机化快速排序的时间复杂度可以通过以下公式表示:
\[ T(n) = O(n) + T(k) + T(n - k - 1) \]
其中:
- \( O(n) \)$ 是分区操作的时间
- \( T(k)\)是排序左侧子数组的时间
- \( T(n - k - 1)\) 是排序右侧子数组的时间
- \( k\) 是基准值左侧的元素数量
在随机化版本中,\(k\) 的期望值是 \(n/2\),因此期望时间复杂度为:
\[ E[T(n)] = O(n \log n) \]
随机化快速排序的变体与优化
1. 三路快速排序
当数组中包含大量重复元素时,传统的两路快速排序效率不高。三路快速排序将数组分为三部分:小于基准值、等于基准值和大于基准值。
实例
"""三路随机化快速排序"""
if low is None:
low = 0
if high is None:
high = len(arr) - 1
if low < high:
# 随机选择基准值
random_index = random.randint(low, high)
arr[random_index], arr[low] = arr[low], arr[random_index]
pivot = arr[low]
# 三路分区
lt = low # 小于基准值的区域边界
gt = high # 大于基准值的区域边界
i = low + 1 # 当前检查的元素
while i <= gt:
if arr[i] < pivot:
arr[lt], arr[i] = arr[i], arr[lt]
lt += 1
i += 1
elif arr[i] > pivot:
arr[i], arr[gt] = arr[gt], arr[i]
gt -= 1
else:
i += 1
# 递归排序小于和大于基准值的部分
randomized_three_way_quick_sort(arr, low, lt - 1)
randomized_three_way_quick_sort(arr, gt + 1, high)
return arr
# 测试包含重复元素的数据
test_data_with_duplicates = [3, 6, 3, 8, 1, 3, 6, 1]
print("原始数组(含重复元素):", test_data_with_duplicates)
print("三路快速排序后:", randomized_three_way_quick_sort(test_data_with_duplicates.copy()))
2. 小数组优化
对于非常小的数组(通常小于 10-20 个元素),插入排序可能比快速排序更高效。我们可以结合两种算法的优点:
实例
"""优化版随机化快速排序:小数组使用插入排序"""
if low is None:
low = 0
if high is None:
high = len(arr) - 1
# 小数组使用插入排序
if high - low + 1 <= threshold:
insertion_sort(arr, low, high)
return arr
if low < high:
pivot_index = randomized_partition(arr, low, high)
optimized_randomized_quick_sort(arr, low, pivot_index - 1, threshold)
optimized_randomized_quick_sort(arr, pivot_index + 1, high, threshold)
return arr
def insertion_sort(arr, low, high):
"""插入排序,用于排序小数组"""
for i in range(low + 1, high + 1):
key = arr[i]
j = i - 1
while j >= low and arr[j] > key:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
# 测试小数组优化
small_test_data = [9, 3, 7, 1, 5, 2, 8, 4, 6]
print("原始小数组:", small_test_data)
print("优化排序后:", optimized_randomized_quick_sort(small_test_data.copy(), threshold=5))
性能对比与实践建议
性能测试
让我们通过实际测试来比较不同排序算法的性能:
实例
import random as rand
def performance_test():
"""性能测试:比较不同排序算法的执行时间"""
algorithms = {
"随机化快速排序": randomized_quick_sort,
"三路快速排序": randomized_three_way_quick_sort,
"优化版快速排序": optimized_randomized_quick_sort,
}
# 生成测试数据
test_sizes = [100, 1000, 10000]
for size in test_sizes:
print(f"\n测试数组大小: {size}")
# 生成不同类型的测试数据
test_cases = {
"随机数据": [rand.randint(0, 10000) for _ in range(size)],
"已排序数据": list(range(size)),
"逆序数据": list(range(size, 0, -1)),
"大量重复数据": [rand.randint(0, 10) for _ in range(size)],
}
for case_name, test_data in test_cases.items():
print(f" {case_name}:")
for algo_name, algo_func in algorithms.items():
data_copy = test_data.copy()
start_time = time.time()
algo_func(data_copy)
end_time = time.time()
execution_time = (end_time - start_time) * 1000 # 转换为毫秒
print(f" {algo_name}: {execution_time:.2f} ms")
# 运行性能测试(注意:对于大数组,这可能需要一些时间)
# performance_test()
